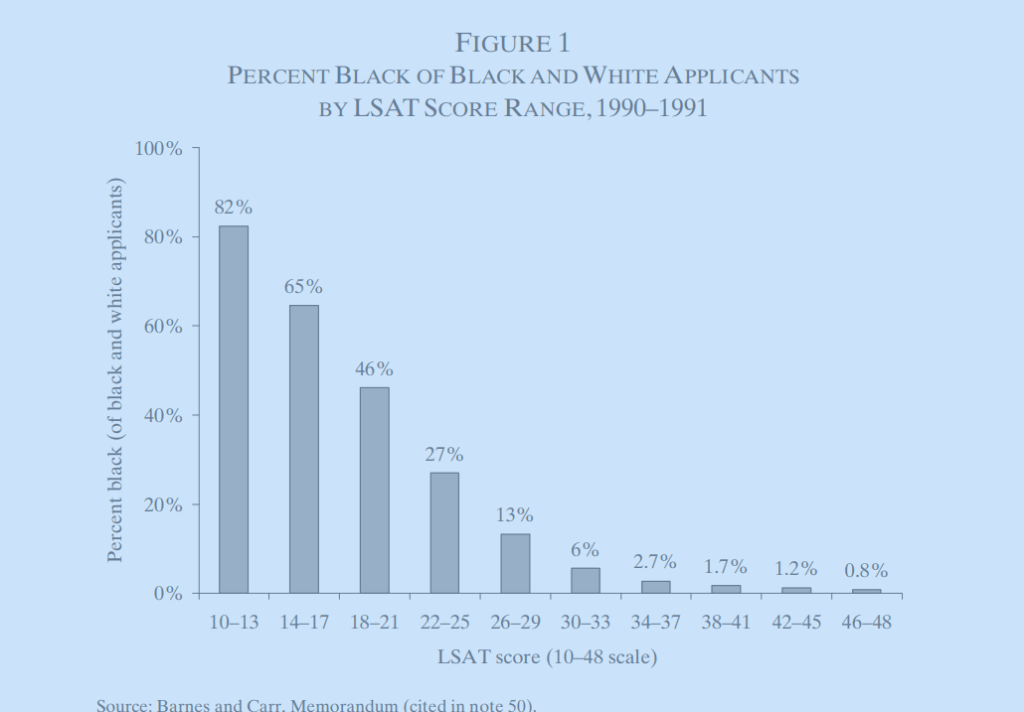
From 1981 to 1991, the LSAT was scored on a scale where 10 was the lowest possible score, and 48 was the highest. In the below chart, we see how various scores equated to percentile rank among those who took the LSAT (an elite sample):

From the above data, our best estimate is LSAT takers had a mean score of 32.6 with an SD of 6.3.

In this article I once again try to convert these scores to IQ but this time using equipercentile equating, a technique in which I will map LSAT scores to IQ by equating both distributions in a sample that took both tests.

I am aware of only nine people with both reported LSAT scores on this scale, and reported scores on tests that can be converted to IQ. Some of these are from famous people (Barack Obama, Eliot Spitzer, Lion of the Blogospher) but most are from the Omni magazine sample used to norm Ron Hoeflin’s Mega Test, though only when there was no score from a more established test (SAT/GRE) with which which to pair the LSAT score, did I use the Mega Test score

For these nine individuals, the correlation between the LSAT and another IQ test they took was about 0.53. Their average LSAT score is 41.5 (SD = 4.5) and their average IQ is 142 (SD = 13).

Thus the formula for converting LSATs from this era to IQ (U.S. norms):

IQ = [(LSAT – 41.5)/4.5](13) + 142

Recall from above that the mean LSAT scores of LSAT takers was 32.6 (SD = 6.3). Thus on a scale where Americans on the whole have an average IQ of 100 (SD = 15), the law school bound elite had averaged IQ 116 (SD 18.9). An average IQ of 116 sounds plausible given that this was just over the mean for college grads in the 1980s but the SD of 18.9 is surprisingly high and may be an artifact of some kind.

Hoeflin writes:

It is most remarkable that Hoeflin got data on the combined SATs of all FIVE MILLION people who took the SAT from 1984 to 1988. I wonder how he was able to get it. This makes the Mega Test potentially the best normed test of all time.

Hoeflin continues:

How did he arrive at 15 million 18-year-olds from 1984 to 1988? According to a USA Today article published June 12th, 2020:

That’s a grand total of 17,960,389 babies born from 1966 to 1970. Of course not all of these babies would have lived long enough to be 18 from 1984 to 1988. According to an article in the Chicago Tribune , about 10% of Americans born 1966 to 1970 were dead by 2021. Even if we absurdly assume, all of them died before 1984 to 1988, that would still leave 16,164,350 alive by those years. Perhaps about a million emigrated, but I suspect they would have been more than replaced by all the kids who immigrated.

I realize Hoeflin may have rounded down to 15 million for simplicity and this my not ave affected the IQs he assigned all that much, but when you create the Mega test; Mega for million because he wanted to identify scores with one in a million rarity, it helps if his denominator is not off by a million.

I can not find a single published study correlating the LSAT with any other intelligence test although the data certainly exists. For example a 1985 study found a 0.72 correlation between LSAT and SATs in 5,854 students, though whether this study was ever published and where, I know not.

From 1948 to 1981, the LSAT was scored using a 200 to 800 point scale similar to the sub-scales of the SAT. Then from 1981 to 1991, it used a 48 point scale. Then starting in 1991, scores were expressed using a 120 to 180 scale. It is this latest version that I discuss in this article.

According to wikipedia: “Although the exact percentile of a given score will vary slightly between examinations, there tends to be little variance. The 50th percentile is typically a score of about 151; the 90th percentile is around 165 and the 99th is about 173. A 178 or better usually places the examinee in the 99.9th percentile.”

In other words, assuming a bellish curve, LSAT takers have an LSAT mean of about 152.1 and an SD of about 8.8.

Here’s a reddit thread where people listed their scores on both the LSAT and the ACT/SAT.

Because the SAT is constantly changing, I decided to focus on the LSAT-ACT correlation, ignoring the SAT.

The correlation between self-reported LSAT scores and ACT scores was +0.47 (n = 21).

Because I know a lot more about how SAT scores relate to IQ than I do about how ACT scores do, I converted all the ACT score to IQ using table A.1 from a 1999 paper by Neil J. Dorans:

The LSAT scores of the sample had a mean of 163 (SD 9.03) and the ACTs converted to SATs scores had a mean of 1307 (SD 161). Then using my formula for converting the post-April 1995 to pre-March 2016 SAT to IQ (IQ equivalent = 23.835 + 0.081(SAT score)) the sample had a mean IQ of 130 (SD 13).

Thus, the formula for equating LSAT to IQ (U.S.) norms:

IQ = [(LSAT – 163)/9.03](13) + 130

Recall that above we estimated LSAT takers have an LSAT mean of about 152.1 and an SD of about 8.8. So on the standard scale where Americans average IQ 100 with an SD of 15, the law school-bound elite average IQ 114 with an SD of 12.7, at least in the recent decades.

Using LSAC demographic data from the library of Congress, Alan R. Lockwood deduced that Barack Obama scored about 43 out of 48 on the LSAT in 1987-88.

I recently came across a paper that looked at all the LSAT scores of all the black and white applicants of law school from around this time and it showed what percentage of applicants above each level were black (see Figure 1 below).

Now in 1990, there were 30 million black Americans and about 200 million white Americans. Thus blacks were 13% of the combined population of both races, however from looking at figure 1, we see blacks were 82% of those with LSAT scores of 13 or lower yet only 0.8 of those with LSAT scores of 46 or higher . So it seems the higher the score, the smaller the percentage of blacks.

Now those with LSAT scores of 26-29 are 13% black, exactly the percentage you’d have found in a random sample of whites and blacks. This tells me that people with LSAT scores in this range reflect a random sample of American IQ, so we can assign the mid-point of this range, 27.5, an IQ of 100 (U.S. norms).

The next question is what IQ do we assign to those with scores of 46+. On a scale where all Americans average IQ 100 with a standard deviation of 15, white Americans averaged about 102 with an SD of 14, and their black counterparts averaged about 89 with an SD of about 14 (see Figure 9 below). Given these statistics and given that whites outnumbered blacks about, 6.66 to one, an LSAT score of 46 would have to equal IQ 135 in order for blacks to be 0.8% of those with scores of 46+

So having assigned an LSAT score of 27.5 an IQ of 100 and a score of 46 an IQ of 135 (+2.33 SD), we can estimate that if a random sample of 22-year-old Americans had taken the LSAT (with sufficient test prep), instead of the law school bound elite, the mean would have been 27.5 and the SD would have been 7.9 which would make Obama’s approximate score of 43 equal to IQ 129 (U.S. norms).

The fact that 43 = IQ 129 is further validated by the fact that 43 was at the 95th percentile of LSAT takers and Mensa equates LSAT scores at the 95th percentile of the LSAT population with the 98th percentile of Americans on the whole which it in turn equates to IQ 130.

An IQ of 129 is further validated by  a former “CIA” guy‘s claims that Chinese spies found Obama’s childhood IQ (as measured by the WISC) to have been 128 (somewhat lower when you adjust for old norms)

Another day, another legend lost. The great Phil Donahue who towered as the #1 talk show in America from the late 1960s to the mid 1980s has passed away at the age of 88. In today’s fragmented media age, where no one star can shine too brightly, it’s easy to forget just how big a star Phil Donahue really was.

Long before social media, streaming, and hundreds of cable channels, everyone in America just watched broadcast television, and pretty much the same few channels at that, so at his peak, probably about one in 20 American adults were watching Donahue on any given weekday, giving hosts like Donahue and his successor Oprah, a level of influence on society that was comparable to that of a United States President.

This was the true golden age of America.

Today everyone and their mother has some kind of kind of talk show in the form of YouTube, podcasts, or just tic-toc videos, so it’s easy to forget what it was like when only the absolute best and brightest held the microphone.

I finally took a look at the statistics of the readers who took the PAIS Information subtest; in particular, the subset of 18 who also reported Wechsler IQ scores (r = 0.43).

The PAIS Information was originally normed on 16 native born English speaking Canadians at a local pool hall and these had a mean of 12 (SD 3.4). However because Canadians are a bit smarter and less variable than Americans, this was adjusted to 11.3 (SD 3.5) to be comparable with the U.S. norms of the Wechsler. These norms may underestimate the IQs of my readers because the readers took the test on computers and thus had to spell the answers, while the pool hall sample just had to say them. While I tried to allow for common spelling mistakes, I could not anticipate all the misspellings that would occur.

On the other hand, the norms my overestimate the IQ of my readers because from reading my blog or sharing my interests, my blog readers know a lot of the stuff that I know which gave them a bit of an advantage over the pool hall sample. These two biases largely cancel each other out.

If we equate 11.3 with IQ 100 and 3.5 with 15 IQ points, then the 18 blog readers have a mean of 137 (SD 14.6), only 6 points higher than their self-reported Wechsler scores. However the real difference between the two norming methods becomes much greater at the extremes.

Using the pool hall derived data, the 18 readers have an IQ range of 103 to 163 but using the range of their Wechsler scores, they have a range of 103 to 150.

It seems the two methods give similar results close to IQ 100 but become increasingly divergent at the extremes. What explains this? Although both methods define IQ as Z(15) + 100, Wechsler IQs are largely derived from normalized Zs, that is Z scores that are FORCED to fit the bell curve. while the other method calculated Z scores normally. It seems that when you force IQ (and many other trait for that matter) to fit a bell curve, you limit variation at the extremes. For example, before the Wechsler scales started forcing scores to fit the normal curve, he noted they showed a Pearson IV distribution, though this had little effect on the vast majority of IQs..

Childhood age ratio IQs where IQ is just your mental age calculated as a percentage of your chronological age yield IQs as high as the 220s! Jensen argued that IQ is normally distributed from 50 to 150 but beyond these extremes, there’s are more people than the normal curve predicts. John Scoville hypothesized that childhood ratio IQs might follow a log-normal distribution causing the distribution to appear normal at the middle of the curve, but deviate as one moves to the extremes.

My own intuition tells me that non-normal distributions might be an artifact of using culturally loaded/crystallized tests. There might be something about biologically extreme minds ending up in culturally extreme environments that causes the surplus at the tails of the curve.

A 1959 psychology thesis by Jame L Holleman examined the WAIS verbal IQs of 46 subjects who took the GRE at Texas Technological College during October 1958. Age range: 20 to 57; mean age: 27; mode: 22.

For unexplained reasons, two items from the WAIS Comprehension subtest were replaced with comparable items from the ancient WBI however that would have had little effect on the entire verbal IQ which is derived from all six verbal subtests.

Table III from the thesis does not report the WAIS verbal IQs of these GRE takers however it does report their WAIS sum of verbal scaled scores: mean: 76.6 (SD 9.54). For ages 20 to 24 and 25 to 34, the WAIS national standardization sample (year: 1953 – 54) had scores of 59.47 (SD 15.21) and 60.82 (SD 14.61) respectively (WAIS manual, page 19)(the figure 58.04 in table III seems to be a typo but the difference is trivial).

Thus these GRE takers had WAIS verbal IQs averaging 117 (SD 9.4) or 117 (9.79) depending which age group they fit more neatly into. Let’s split the difference and say 117 (SD 9.6). One could arguably deduct about 1 IQ point for the slightly older verbal WAIS norms (Flynn effect).

Using the logic of equipercentile equating/score pairing, we can draw some rough conclusions:

GRE verbal 458 = IQ 117 (U.S. norms) and every 105 points above or below adds or subtracts 9.6 points.

GRE combined (V + Q) = 950 = IQ 117 and every 180 points above or below adds or subtracts 9.6 points.

Prior to May 1994, Mensa accepts a combined V+Q GRE of 1250 which by my formula would equate to an IQ of 133 (very close to Mensa’s advertised cut-off of 130 especially if we shave off a few IQ points for any GRE Flynn effect from the 1958 to 1994).

From 1965 to 1989, the GRE population went from having a verbal mean of 530 (SD = 124) to 484 (SD 125) which roughly equates to going from IQ 124 (SD 11.34) to 119 (SD 11.43) so even though elite graduate schools were becoming more selective, the applicant pool from which they were selecting were getting dumber, so the average IQ of Ivy League grad students was probably not changing much.

The following is an interesting paragraph from Matarazzo & Goldstein (1972):

Not sure if this says more about the relevance of grades or the validity of the original WAIS (at least at the high end).

Based on thousands of people who took both the SAT and GRE in the 1980s, we can say that a verbal GRE of 510.1 (SD 107.7) equaled an SAT verbal of 518.8 (SD 104.7)

By the end of the 1980s, the average GRE taker 484 SD 125 (source)

From the above data points, we can say GRE takers had the equivalent of a verbal SAT of 493 (SD 122).

Now national norms studies suggest that if all American young adults had taken the SAT in the 1980s (not just the college-bound elite), the verbal mean and SD respectively would be 376 and 102 (Herrnstein & Murray 1994). If the U.S. mean is defined as 100 and 15 respectively, this puts the 1980s GRE population at 117 and 18.

[UPDATE July 25, 2024: A commenter suggested that the strangely high standard deviation of the GRE takers was inflated by the uneven verbal scores of foreign test takers. I thus re-did the analysis using the math SAT and this time I got a slightly lower mean IQ (116) but oddly an even bigger SD (19). ]